Merkle Sum Tree Block Structure¶
One of the most important improvements Plasma Cash introduced was “light proofs.” Previously, plasma constructions required that users download the entire plasma chain to ensure safety of their funds. With Plasma Cash, they only have to download the branches of a Merkle tree relevant to their own funds.
This was accomplished by introducing a new transaction validity condition: transactions of a particular coinID are only valid at the coinIDth leaf in the Merkle tree. Thus, it is sufficient to download just that branch to be confident no valid transaction exists for that coin. The problem with this scheme is that transactions are “stuck” at this denomination: if you want to transact multiple coins, you need multiple transactions, one at each leaf.
Unfortunately, if we put the range-based transactions into branches of a regular Merkle tree, light proofs would become insecure. This is because having one branch does not guarantee that others don’t intersect:

Leaves 4 and 6 both describe transactions over the range (3,4). Having one branch DOES NOT guarantee that the other doesn’t exist.
With a regular Merkle tree, the only way to guarantee no other branches intersect is to download them all and check. But that’s no longer a light proof!
At the heart of our plasma implementation is a new block structure, and an accompanying new transaction validity condition, which allows us to get light proofs for range-based transactions. The block structure is called a Merkle sum tree, where next to each hash is a sum value.
The new validity condition uses the sum values for a particular branch to compute a a start and end range. This calculation is specially crafted so that it is impossible for two branches’ computed ranges to overlap. A transfer is only valid if its own range is within that range, so this gets us back our light clients!
This section will specify the exact spec of the sum tree, what the range calculation actually is, and how we actually construct a tree which satisfies the range calculation. For a more detailed background and motivation on the research which led us to this spec, feel free check out this post.
We have written two implementations of the plasma Merkle sum tree: one done in a database for the operator, and another in-memory for testing in plasma-utils.
Sum Tree Node Specification¶
Each node in the Merkle sum tree is 48 bytes, as follows:
[32 byte hash][16 byte sum]
It’s not a coincidence that the sum’s 16 bytes length is the same as a coinID!
We have two helper properties, .hash and .sum, which pull out these two parts. For example, for some node = 0x1b2e79791f28c27ed669f257397e1deb3e522cf1f27024c161b619d276a25315ffffffffffffffffffffffffffffffff, we have
node.hash == 0x1b2e79791f28c27ed669f257397e1deb3e522cf1f27024c161b619d276a25315 and node.sum == 0xffffffffffffffffffffffffffffffff.
Parent Calculation¶
In a regular Merkle tree, we construct a binary tree of hash nodes, up to a single root node. Specifying the sum tree format is a simple matter of defining the parent(left, right) calculation function which accepts the two siblings as arguments. For example, a regular Merkle sum tree has: .. code-block:: javascript
parent = function (left, right) { return Sha3(left.concat(right)) }
Where Sha3 is the hash function and concat appends the two values together. To create a merkle sum tree, the parent function must also concatenate the result of an addition operation on its children’s own ``su
parent = function (left, right) { return Sha3(left.concat(right)).concat(left.sum + right.sum) }
For example, we might have
parent(0xabc…0001, 0xdef…0002) ===
hash(0xabc…0001.concat(0xdef…0002)).concat(0001 + 0002) ===
0x123…0003
Note that the parent.hash is a commitment to each sibling.sum as well as the hashes: we hash the full 96 bytes of both.
Calculating a Branch’s Range¶
The reason we use a merkle sum tree is because it allows us to calculate a specific range which a branch describes, and be 100% confident that no other valid branches exist which overlap that range.
We calculate this range by adding up a leftSum and rightSum going up the branch. Initializing both to 0, at each parent verification, if the leaf lies somewhere under the left child, we take rightSum += right.sum, and if the leaf is under the right, we add leftSum += left.sum.
Then, the range the branch describes is (leftSum, root.sum - rightSum). See the following example:

In this example, branch 6’s valid range is [21+3, 36–5) == [24, 31). Notice that 31–24=7, which is the sum value for leaf 6! Similarly, branch 5’s valid range is [21, 36-(7+5)) == [21, 24). Notice that its end is the same as branch 6’s start!
If you play around with it, you’ll see that it’s impossible to construct a Merkle sum tree with two different branches covering the same range. At some level of the tree, the sum would have to be broken! Go ahead, try to “trick” leaf 5 or 6 by making another branch that intersects the range (4.5,6). Filling in only the ``?``s in grey boxes:

You’ll see it’s always impossible at some level of the tree:

This is how we get light clients. We call the branch range bounds the implicitStart and implicitEnd, because they are calculated “implicitly” from the inclusion proof. We have a branch checker implemented in plasma-utils via calculateRootAndBounds() for testing and client-side proof checking:
let leftSum = new BigNum(0) let rightSum = new BigNum(0) for (let i = 0; i < inclusionProof.length; i++) {
let encodedSibling = inclusionProof[i] if (path[i] === ‘0’) {
computedNode = PlasmaMerkleSumTree.parent(computedNode, sibling) rightSum = rightSum.add(sibling.sum)
- } else {
- computedNode = PlasmaMerkleSumTree.parent(sibling, computedNode) leftSum = leftSum.add(sibling.sum)
}
}
as well as in Vyper for the smart contract via checkTransferProofAndGetTypedBounds in PlasmaChain.vy
Parsing Transfers as Leaves¶
In a regular merkle tree, we construct the bottom layer of nodes by hashing the “leaves”:
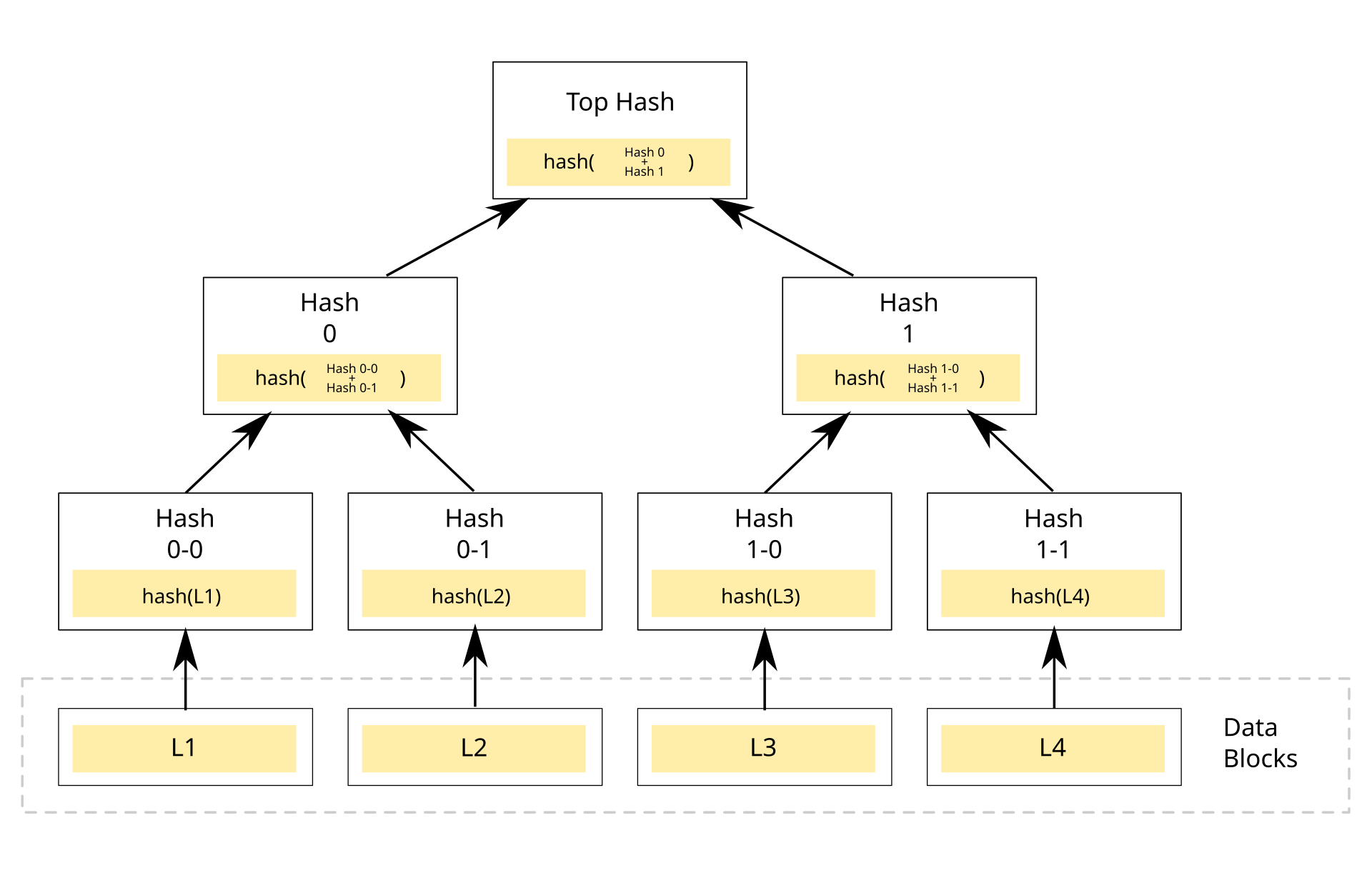
In our case, we want the leaves to be the transactions of ranges of coins. More specifically, we actually want `Transfer`s–signatures don’t need to be included, they can be stored by the clients and submitted to the smart contract separately. (For more details on objects and serialization, see the serialization section.)
So–the hashing is straightforward–but what should the bottom nodes’ .sum values be?
Given some txA with a single transferA, what should the sum value be? It turns out, _not_ just transferA.end - transferA.start. The reason for this is that it might screw up other branches’ ranges if the transfers are not touching. We need to “pad” the sum values to account for this gap, or the root.sum will be too small.
Interestingly, this is a non-deterministic choice because you can pad either the node to the right or left of the gap. We’ve chosen the following “left-aligned” scheme for parsing leaves into blocks:

We call the bottommost .sum value the parsedSum for that branch, and the TransferProof schema includes a .parsedSum value which is used to reconstruct the bottom node.
Branch Validity and Implicit NoTx¶
Thus, the validity condition for a branch as checked by the smart contract is as follows: implicitStart <= transfer.start < transfer.end <= implicitEnd . Note that, in the original design of the sum tree in Plasma Cashflow, some leaves were filled with NoTx to represent that ranges were not transacted. With this format, any coins which are not transacted are simply those between (implicitStart, transfer.start) and (transfer.end, implicitEnd). The smart contract guarantees that no coins in these ranges can be used in any challenge or response to an exit.
Atomic Multisends¶
Often (to support transaction fees and exchange) transactions require multiple transfers to occur or not, atomically, to be valid. The effect is that a valid transaction needs to be included once for each of its .transfers - each with a valid sum in relation to that particular transfer.typedStart and .typedEnd. However, for each of these inclusions, it’s still the hash of the full UnsignedTransaction - NOT the individual Transfer- that is parsed to the bottom .hash.